Introduction
Multiple structure alignment tools (MSAs) are necessary to obtain a simultaneous comparison of a family of related folds. In this study, we have developed a method for multiple structure comparison largely based on sequence alignment techniques. A widely used Structural Alphabet named Protein Blocks (PBs) was used to transform the information on 3D protein backbone conformation as a 1D sequence string. A progressive alignment strategy similar to CLUSTALW was adopted for multiple PB sequence alignment (mulPBA). Highly similar stretches identified by the pairwise alignments are given higher weights during the alignment. The residue equivalences from PB based alignments are used to obtain a three dimensional fit of the structures followed by an iterative refinement of the structural superposition. Systematic comparisons using benchmark datasets of MSAs underlines that the alignment quality is better than MULTIPROT, MUSTANG and the alignments in HOMSTRAD, in more than 85% of the cases. Comparison with other rigid-body and flexible MSAs also indicate that mulPBA alignments are superior to most of the rigid-body MSAs and highly comparable to the flexible alignment methods.
Principle:
The protein structures are first encoded as a series of PBs (see 1), then pairwise comparisons are carried out using iPBA methodology (see 2) [Joseph et al. 2010]. In the second step, a dendogram tree is computed (see 3) based on pairwise PB identities and PB sequences are progressively aligned to generate a multiple PB sequence alignment (see 4). This 'sequence-like' alignment is then translated into a 3D structural fit.
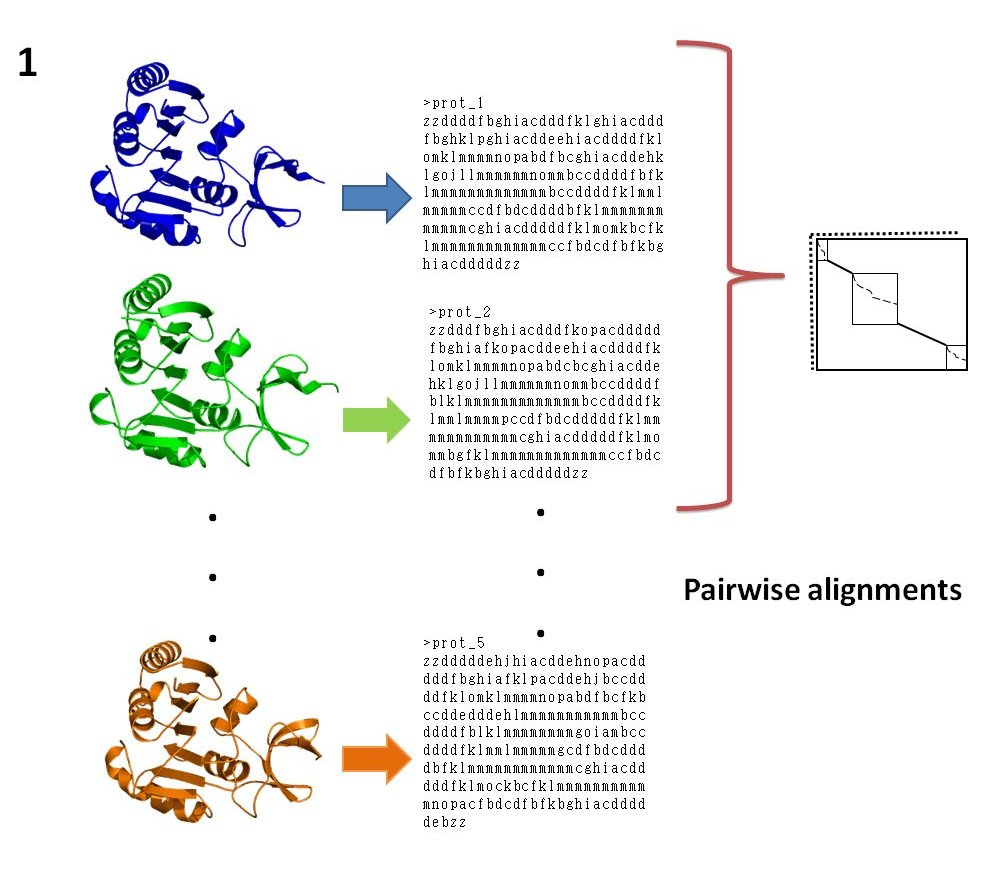
Method in detail: The protein structures to be aligned are first translated into PB sequences (see 1). The pairwise alignments are obtained using iPBA which performs an anchor based alignment by finding structurally conserved regions, identified as local alignments [iPBA]. A combination of local and global dynamic programming algorithms is used for the alignment. A set of local alignments (anchors) associated with these two sequences is derived using a modified version of SIM algorithm. The remaining segments between anchors (linkers) are then aligned with relaxed gap penalties, using Needleman-Wunsch algorithm. The PB substitution matrix was generated using substitution frequencies obtained from alignments of domain pairs in PALI [PALI] with no more than 40% sequence identity. The PB identities calculated from pairwise alignments were translated into a distance matrix (see 2). The matrix was then used to generate a guide tree (see 3) and the tree root was identified by mid-point rooting method. Each sequence was assigned a weight depending on the distance from the root. It reduces the bias due to variation in the extent of similarity between the sequences.
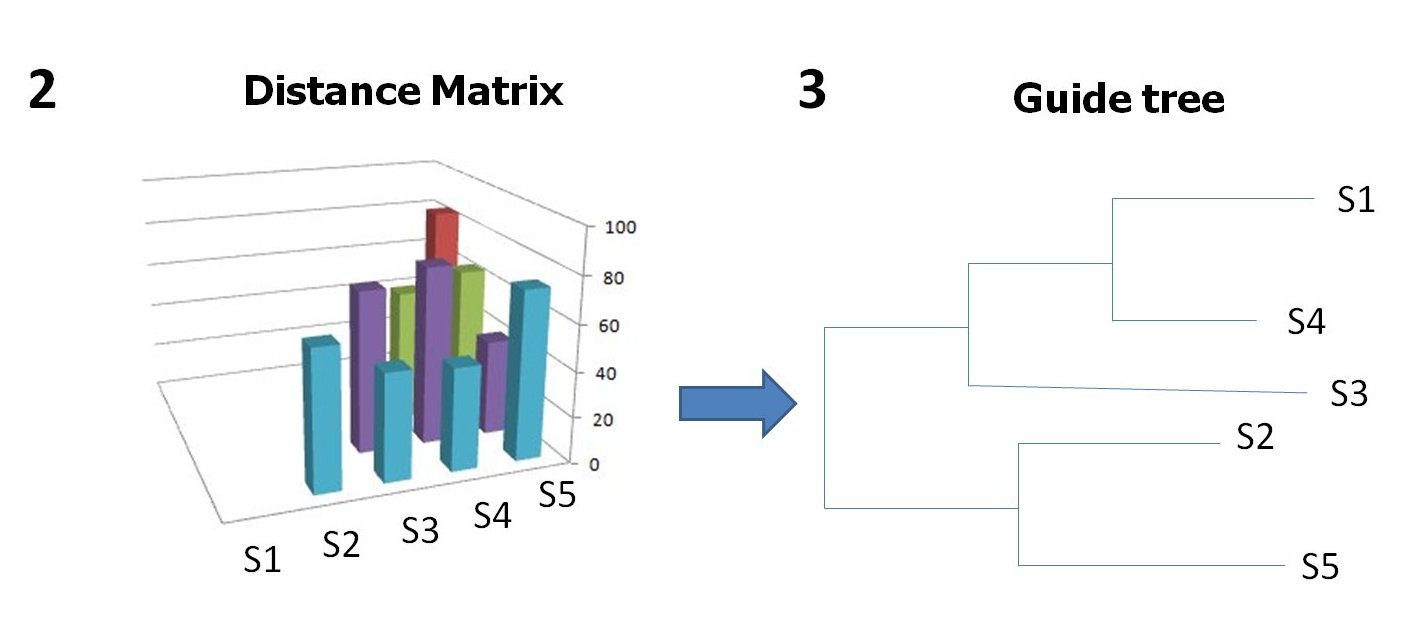
The tree was used to guide the assembly of sequences based on the degree of similarity, to form the multiple alignment. The alignment of two sequences (or groups of sequences) is carried out using dynamic programming. The average of pairwise PB substitution scores (from the substitution matrix) was used to calculate the score for aligning an element (alignment column) of a sequence group against an element (alignment column) of another. These scores S were weighted using sequence weights obtained from the guide tree. While aligning two profiles P1 and P2 of sizes k and l, the score for substituting a column i of P1 with column j of P2 is given by:
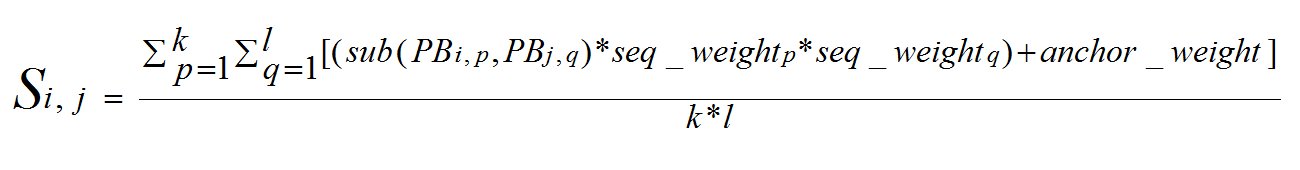
seq_weightp and seq_weightq indicates the sequence weights assigned based on the guide tree, to the sequence corresponding to p and q respectively. From each pairwise alignment used for obtaining the guide tree, the positions corresponding to the alignments in the structurally similar regions (anchors), were stored. These positions were then assigned a weight, namely anchor_weight, which is calculated as: anchor_weight = 250*(1+cov) where cov indicates the percentage coverage of the anchor with respect to the alignment length.
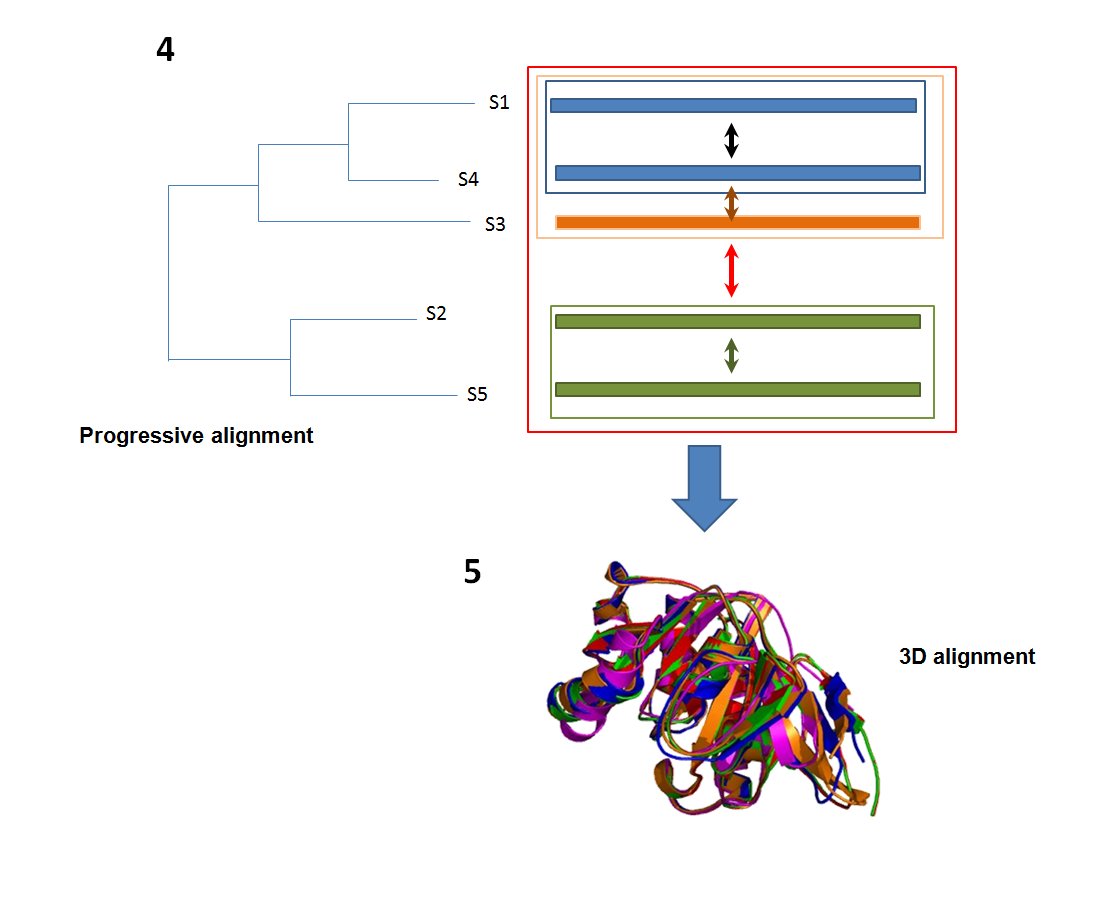
The multiple PB sequence alignment obtained (see 4) is used as an input to PROFIT [link] ], to obtain the 3D superimposition (see 5).
References
- J.-C. Gelly, Joseph A.P., Srinivasan N., de Brevern A.G. 2010. iPBA : A tool for protein structure comparison using sequence alignment strategies Nucleic Acid Res 39:W18-23.[pubmed]
- Joseph A.P., Srinivasan N., de Brevern A.G. 2010. Improvement of protein structure comparison using a structural alphabet. Biochimie 93(9):1434-45.[pubmed]
- Thompson J.D., Higgins D.G., Gibson T.J . 1994. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22(22): 4673–4680.[pubmed]
- Gowri, V. S., Pandit, S. B., Karthik, P. S. Srinivasan, N., Balaji, S. 2003. Integration of related sequences with protein three-dimensional structural families in an updated Version of PALI database. Nucleic Acids Res. 2003 31: 486-488.[pubmed]
- Sujatha, S., Balaji, S. Srinivasan, N. 2001. PALI-a database of alignments and phylogeny of homologous protein structures. Bioinformatics 2001 17: 375-376.[pubmed]
- Balaji, S., Sujatha, S., Kumar, S.S.C., Srinivasan, N. 2001. PALI-a database of alignments and phylogeny of homologous protein structures. Nucleic Acids Res. 2001 29: 61-65.[pubmed]
- de Brevern, A.G., Etchebest, C., and Hazout, S. 2000. Bayesian probabilistic approach for predicting backbone structures in terms of protein blocks. Proteins 41: 271-287.[pubmed]
- Huang, X., Miller, W. 1991. A time-efficient linear-space local similarity algorithm. Advances in Applied Mathematics 12: 337 - 357.[article]
- Joseph, A.P., Agarwal, G., Mahajan, S., Gelly, J.C., Swapna, L.S., Offmann, B., and Cadet, F. 2010. A short survey on protein blocks. Biophys Rev 2: 137-145.[article]
- Needleman, S.B., and Wunsch, C.D. 1970. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J Mol Biol 48: 443-453.[pubmed]
- Smith, T.F., and Waterman, M.S. 1981. Identification of common molecular subsequences. J Mol Biol 147: 195-197.[pubmed]
- Tyagi, M., de Brevern, A.G., Srinivasan, N., and Offmann, B. 2008. Protein structure mining using a structural alphabet. Proteins 71: 920-937.[pubmed]
- Tyagi, M., Gowri, V.S., Srinivasan, N., de Brevern, A.G., and Offmann, B. 2006. A substitution matrix for structural alphabet based on structural alignment of homologous proteins and its applications. Proteins 65: 32-39.[pubmed]
- Zemla, A. 2003. LGA: A method for finding 3D similarities in protein structures. Nucleic Acids Res 31: 3370-3374.[pubmed]