Introduction
The 3D structure of a protein is the main physical support of a protein's biological function. 3D protein folds are primarily maintained through interactions (energetic aspect) between amino acids. Inter-residue contacts (geometric aspects) are essential for the stability of protein folds. Therefore, many methodologies dealing with structure analysis, structure prediction, and structure-function relationships are based on residue contact analyses. Usually, these contacts are defined by a distance threshold (Faure et al., 2008). Here, we use an alternative method, based on Laguerre (Weighted Voronoi) diagrams (Esque et al., 2010; Esque et al., 2011). This approach defines contacts in a more adaptable, scale free, manner. Computed values, e.g., residue volumes fitted with well experimental data (Esque et al., 2010).
VLDP (Voronoi Laguerre Delaunay Protein) Method
A Voronoi/Laguerre tessellation is a partition of space into polyhedra, each one enclosing an atom of the data set (protein), whereas the dual diagram, called Delaunay, builds a graph with vertices at the atom centres. These graphs define nearest neighbours, whence contacts, for each points of the data set. It can be proved that both methods, the standard Voronoi (G.F. Voronoi, 1908), and the weighted, or Laguerre, tessellation give a geometrically consistent partition of space. In structural biology, weighted Voronoi-related methods were used to study the protein structures (see Poupon, 2004 for a review).
Voronoi Laguerre Delaunay Protein webserver (VLDPws) first computes the Delaunay diagram (Figure 1A). Given a set E of N points { p1,...,pN }, a Delaunay tetrahedron {p1p2p3p4} is a tetrahedron whose circumscribed sphere contains no other point of the set E than the four vertices p1p2p3p4 (Figure 1A, case in 2D). In VLDPws, the Delaunay diagram is computed using an optimized incremental algorithm, starting from an initial box which is a tetrahedron large enough to contain the entire set of points. Then, the Voronoi/Laguerre diagram (Figures 1B and D) is deduced by duality. The weights can be interpreted as squared radius. Looking at the definition of the radical distance, in Figure 1C, shows that Voronoi diagram is a particular case of Laguerre diagram where the radii are the same.

In this description, the protein appears as a packing of polyhedra (Figure 2B) solvent around the solute is necessary to have a reasonable tessellation throughout the entire system, including the protein surface. Areas and volumes are defined as polygonal face areas and polyhedral volumes for atoms, as sums of these quantities for molecules or entities composed of several atoms. In particular, the Polyhedral Interface Area (PIA) (of a residue or a protein region) is the sum of the areas of the faces separating atoms of the protein from water atoms or molecules (considered as polyhedra), normalised by the total surface of that region. PIA accounts for the degree of exposure, or accessibility, of amino acids. Other algorithms from the graph theory are also implemented : connected components, stratification, connectivity. The Delaunay connectivity (atomic contacts) are directly stored during the building of diagram.
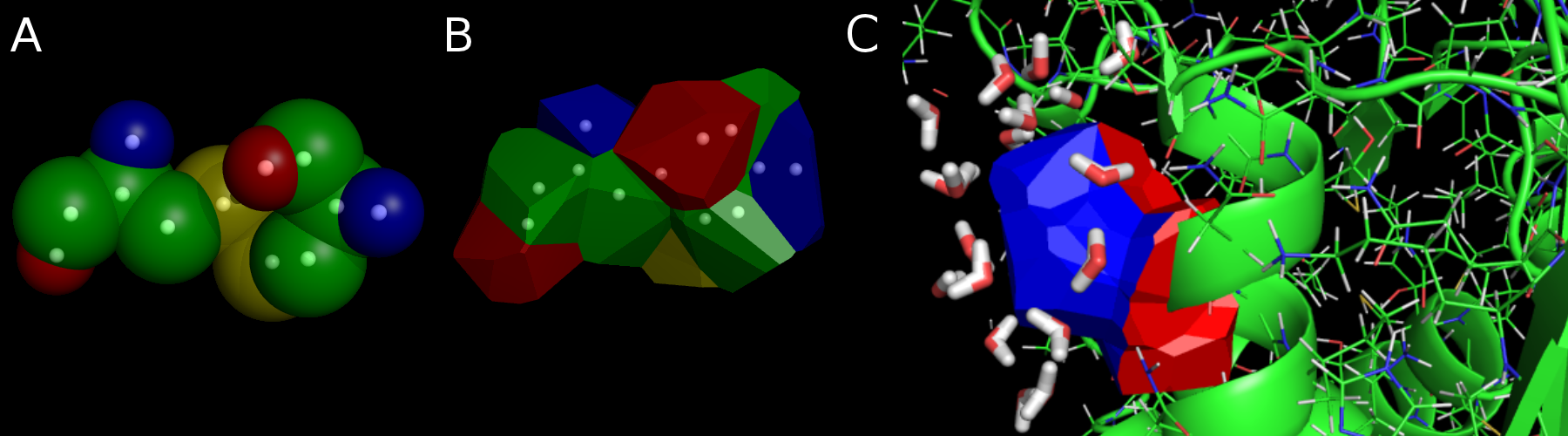 Figure 2. Different representations of a residue: A Van der Waals sphere and Laguerre representations. A. Atomic Van der Waals spheres. B. Laguerre polyhedra (using the same set). C. In the protein, the surface of an amino acid into a part at the water interface (in blue, of area As) and a part buried in the protein (in red, of area Ab). The PIA (Polyhedral Interface Area) is defined as PIA = (As)/(As+Ab)x100.
Figure 2. Different representations of a residue: A Van der Waals sphere and Laguerre representations. A. Atomic Van der Waals spheres. B. Laguerre polyhedra (using the same set). C. In the protein, the surface of an amino acid into a part at the water interface (in blue, of area As) and a part buried in the protein (in red, of area Ab). The PIA (Polyhedral Interface Area) is defined as PIA = (As)/(As+Ab)x100.
VLDPws is a powerful geometric tool for analysing protein structures.
References
- Esque, J., Oguey, C., and de Brevern, A.G. (2010). A novel evaluation of residue and protein volumes by means of Laguerre tessellation. J. Chem. Inf. Model. 50(5):947 - 960.[pubmed]
- Esque, J., Oguey, C., and de Brevern, A.G. (2011). Comparative analysis of threshold and tessellation methods for determining protein contacts. J. Chem. Inf. Model. 51(2):493 - 507.[pubmed]
- Faure G, Bornot A, and de Brevern A.G. (2008). Protein contacts, inter-residue interactions and side-chain modelling. Biochimie 90(4):626 - 639.[pubmed]
- Poupon, A (2004). Voronoi and Voronoi-related tessellations in studies of protein structure and interaction. Curr. Opin. in Struct. Biol. 14:233 – 241.[pubmed]